Study settings and main results
This study covered all equivalent areas in the province 3103 (referred to below in the name of provinces) throughout the adjacent US44. We coordinated the province's borders from 2000 to 2020, taking into account historical changes within the limits of maps. We obtained the monthly death records by the province (with demographic information at the individual level) from the National Center for Health Statistics (2000-2020) and annual population data at the province level according to the age group of the monitoring and epidemic program and the results of the end, the National Cancer Institute 45. Then we calculated normative death rates at the province level using the record population in the United States for the year 2000. Below, the death rates are determined in Age and reporting for every 10 million individuals.
We focused on the 23 category of disease (table 1). The deaths that caused all causes included non -external and external causes, and non -external deaths were ranked more in some infectious and parasitic diseases, mental and behavioral disorders, circulatory system diseases, etc. Other categories have not been evaluated given the sizes of samples. See the examination process in the S1.
The Yale University Institutional Review Council decided that this study does not include human topics (ID: 2000036520).
Exposure evaluation
We extracted the events of the flood during the 2000-2020 set by the National Storm of Oceanic and Calf Pathology database (NOAA), along with the dates of the boycott/starting and end area. The database included all flooding events (except for coastal floods associated with tropical storms (for example, hurricane)) with sufficient intensity to take financial loss and damage to property, injuries or deaths, and merge information from both objective measures (for example, the size of the surplus and information period from the match, emergency management officials) and local media (EG). More details about the flood definition was in the S1 text. As for the encrypted floods as events in the province, we converted the event level data directly into a monthly number at the province level of flooding days. For encrypted floods as logical events, we used the NOAAA-ForeCAST province to determine the location of the affected provinces, and calculate the percentage of the province area, which is affected based on the borders of the area specified by NOAA, then counting the floods at the province level. In the main analysis, we did not have any restrictions on the size of the affected area until the boycott was considered exposed; While in an allergy analysis, we included provinces that are only affected by floods and provinces at the province level by> 20 %, 40 %, 60 %, or 80 % of the province area affected by logical floods. We also calculated the monthly temperature at the boycott level, sedimentation, and snow from the Daymet Dataset46.
Statistical analysis
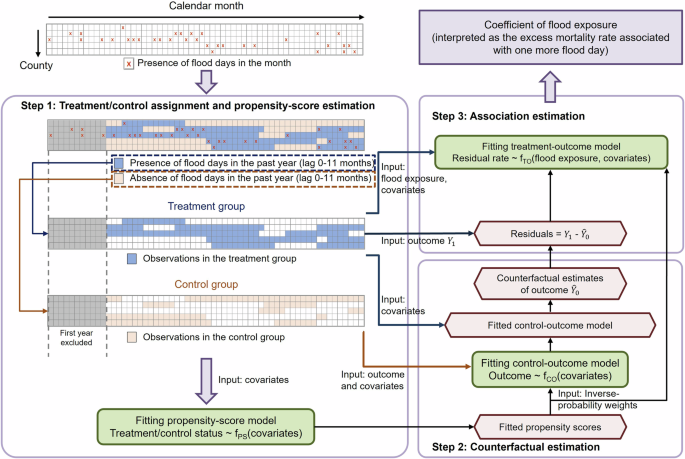
All statistical analyzes were based to 2001 to 2020 (with the exclusion of 2000 due to incomplete exposure records). We applied a strong three-fold approach (Figure 1) using the average movement of the number of monthly flooding days in the following year: (1) We assigned notes in two months of the province in treatment/monitoring groups based on the presence/absence Its associations are generally over 12 months (for example, the connection with deaths for all reasons has reached almost the size On the joint variables (specified below) in the control group using a semi -Bouason slope (the name of the control results). The reverse calculated from the degrees of inclination. We have interpreted the flood coefficient as an additional death rate for an additional monthly flood.
In all models, we controlled meteorological factors including the monthly temperature, rain and snow in that province, the average rainfall and the days Analysis studies the relationship between floods and deaths. In the degree of inclination and control of control results, we included the fixed effects of the provinces, groups of the orthodontic year of the year, and groups of the year and the evaluation to control spatial, temporal and spatial confusion, respectively. More details about choosing common variables and confusing problems were in the S1 text.
Specifically, we used the logistical slope of the tuning degree model as shown below,
$ hanging Condition}}} _ {{\ rm {c}}}, {\ rm}}} {{\ r {m}}} \, \ sim {\ rm {benouli}}}}}}}
(1)
$ hanging rm}}}, {\ rm {a}}}, {\ rm}}} \ right) $$
(2)
where\ ({{\ rm {t}}} {{\ rm {eatment}}}/{\ rm {control \; case}}}} _ {{\ rm {c}}}, {\ rm}}} {\ r}} \) Is the state of treatment/control of the boycott? (C \)In the month \ (M) From a year (A \)and\ (P) It is a possibility to be in the treatment group,\ ({\ alpha} _ {c} \) It is the fixed term for provinces,\ ({\ alpha} _ {s, a} \) It is the fixed term for state groups and the evaluation year,\ ({\ alpha} _ {a, m} \) It is the term fixed effect of public evaluation groups and the month of the year, and \ ({{\ rm {f}}} ({\ rm {covariate}}}} {{\ r {s}}} _ {{{\ r}}}} {{\ rm}}} {\ r}}}) \) Controls on common variables, including monthly temperature, sedimentation, snow in the province itself, average rainfall and flood days in the surrounding provinces (defined as other provinces in the same state).
We installed the control results model using a semi -Bouason slope in the control group distributed by the reverse stability weights based on the degrees of inclination calculated from the tuning degree model.
$$ \ log Right) = {\ alpha} _ {c}+{\ alpha} _ {s, {a}+{\ alpha} _ {a, {m}}+{\ rm}}} \ lEft ({\ r {covariaate}}}} {\ r m {s}}} {{\ r}}}}} {{\ rm {a}}}, {\ rm {m}} \ right \\ +{{\ rm {offset}}} \ left (\ log RM {a}}} \ right)
(3)
where \ ({y} _ {c, {a}, {m}} \) It is the number of monthly delegations modified by age in the province (C \)In the month \ (M) From a year (A \)And \ ({{\ rm {poplaatio}}} {{{\ rm {n}}} _ {{\ rum}}}}}} {{\ r {a}}} \) It is the total population in the province (C \) per annum (A \).
We installed the process of the processing results in the processed processing group by the reverse probability weights based on the degree of inclination calculated from the tunnel degree model.
$$ {{\ rm {rat}}} {{\ rm {e}}} _ {{\ r {c}}} {{\ rm {a}}}, {\ rm}}} _ {0}+{\ beeta} _ {1} {{\ r {floo}} {{\ r}} { {{\ rm {a}}}, {\ rm {m}}}}+{{\ rm}}} \ lEft ({{{{\ rm {covariate}}}} {{{\ rm}}} _ {{\ r}}} {{\ r}}}}}}} Right)+{e} _ {C, A, M} $$
(4)
where\ ({{\ rm {rat}}} {{\ rm {e}}} _ {{\ r {c}}, {{\ rm {a}}, It is the rate of remaining monthly deaths by age in the province (C \)In the month \ (M) From a year (A \) (any, \ (({y} _ {{1} _ {c, {a}, {m}}-{\ hat {y} _ {0} _ {c, {a}, {m}}}) POPULATIO}}}} {{{\ rm}}} _ {{\ r}} {{\ r}}}),\ ({\ hat {y}} _ {0} _ {c, {a}, {m}} \) Is the number of antagonist deaths did not cause floods by communicating the values of joint variables in the treatment group in the control results form,\ ({\ alpha} _ {0} \) It is the intersection,\ ({\ beeta} _ {1} \) It is the laboratories of the moving averages for the monthly charges on the days of the floods (C \)In the month \ (M) From a year (A \) ((\ ({{\ rm {floo}}} {{\ rm {d}}} _ {{\ r {c}}, {{\ r}}}, {\ rm}),and \ ({{\ rm {f}}} ({\ rm {covariate}}}} {{\ r {s}}} _ {{{\ r}}}} {{\ rm}}} {\ r}}}) \) Other joint variables control tools (such as those in the tuning degree model except for fixed effects).
Class analyzes according to the rates with a possible effect
To calculate the differences in the severity of the flood, we conducted a class analysis according to the type of flood (sudden floods against non -virtuous floods). Other types of floods (i.e. coastal floods, lake floods, and debris flows) were not evaluated due to small sample sizes (Specger S1).
We also evaluated different sub-groups by age (0-64 years, ≥ 65 years; there is no more accurate classification in view of the distribution of the sample according to age), sex (male, female), sweat, sweat (non-dark white, non-Manganian, black of Spanish origin, and white of Spanish origin (another sample was excluded). S2). Other causes were not evaluated due to samples. We used the Q-Statistic and P-Value value to describe the inconsistency between the groups.
Looking at the large number of flooding and influential population events and the assumption of causation in our estimates, we calculated the deaths attributed to the floods by collecting the deaths attributed in two months of the province (i.e. the excessive death rate for each flood x average day of flood) on the provinces in the neighboring United States and months 2001-2020.
Allergy Analysis
We conducted many allergies to assess the durability of our initial results: (1) Change the time window: in the main analysis, LAG 0-11 months (for example, exposure to death that occurs in May 2024 will be exposure to floods from June 2023 to May 2024); (2) Changing the terms of the fixed effect to evaluate the possible seasonal approved on the site; (3) Treating extremist values in the weights of reverse possibilities; (4) For logical floods, including provinces that are more than 20 %, 40 %, 60 %, or 80 % of the province area; And (5) With the exception of 2020 data, such as Covid-19.
All statistical analyzes were conducted at R-2.2.0. The fixed slope is installed in the models of the inclination and the control results models using the R “Fixest” package (version 0.11.1). We interpreted P <0.05 as statistically significant and reported according to strong guidelines. Codes are available on https://github.com/chenlab-yale/flood_mortality_us (https://doi.org/10.5281/zenodo.14888416)51.
Report
More information about research design is available in the summary of the nature portfolio associated with this article.